白纸一张

三十而立，四十而不惑

0%

练习项目(十三)：简单地实现PBR

发表于 分类于
本文字数： 7.8k 阅读时长 ≈ 7 分钟

概述

本文主要参考《Unity Shader 入门精要》中改版后的第18章实现基于物理的渲染。之前有很多次，在学习《Unity Shader 入门精要》中的PBR章节和《Learn OpenGL》中的PBR章节时，看到很长的推导篇幅，就望而却步，一直没有比较完整地实现一遍PBR。这次静下心来完整地看了一遍《Unity Shader 入门精要》中改版后的第18章实现基于物理的渲染，发现没有自己想象中的那么复杂。其实基本上都是围绕渲染方程来展开的。这里，不会一步步地推导各种公式、方程，只会给出最终要用到的公式，具体的推导过程，还是推荐看看改版后的第18章。

一、公式

1、渲染方程

从整体上来看，都是围绕渲染方程的： \[ L_o(v)=L_e(v) + \int_{\Omega} f(\omega_i,v)L_i{\omega_i}(n\cdot\omega_i)\, d\omega_i \] 简单地解释一下上面的公式：给的观察视角\(v\)，该方向上的出射辐射率\(L_o(v)\)等于该点向观察方向发出的自发光辐射率\(L_e(v)\)加上所有有效的入射光\(L_i(\omega_i)\)到达观察点的辐射率积分和。下图给出了渲染方程各个部分的通俗解释。

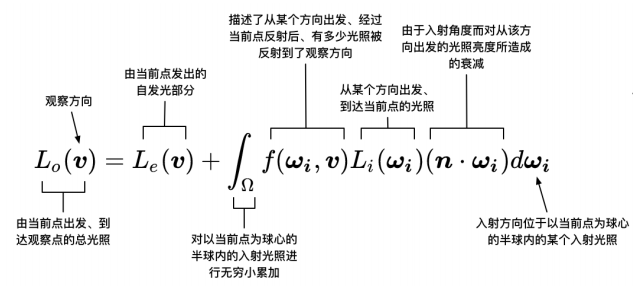
渲染方程式图形学中的核心公式，当去掉其中的自发光项之后，剩余的部分就是著名的反射等式。我们可以这样理解反射等式：想象我们现在要计算表面上某点的出射辐射率，我们已知到该点的观察方向，该点的出射辐射率是由从许多不同方向的入射辐射率叠加后的结果。其中，\(f(\omega_i,v)\)表示了不同方向的入射光在该观察方向上的权重分布。我们把这些不同方向的光辐射率（\((L_i(\omega_i))\)部分）乘以观察方向上所占的权重（\(f(\omega_i,v)\)部分），再乘以它们在该表面的投影结果（\((n\cdot\omega_i)\)部分），最后再把这些值加起来（即积分操作）就是最后的出射辐射率。

在实时渲染中，自发光项通常就是直接加上某个自发光值。除此之外，积分累加部分在实时渲染中也基本无法实现，因此积分部分通常会被若干精确光源的叠加所替代。

2、精确光源

对于一个精确光源来说，我们使用\(l_c\)来表示它的方向，使用\(c_{light}\)表示它的颜色。使用精确光源的最大好处是，我们可以大大简化上面的反射等式，不用计算积分了。我们可以使用下面的等式来计算它在某个观察方向\(v\)上的出射辐射率： \[ L_o(v)=\pi f(l_c,v)c_{light}(n\cdot l_c) \] 和之前使用积分形式的原始公式相比，上面的式子使用一个特定的方向的\(f(l_c,v)\)值来代替积分操作，这大大简化了计算。如果场景中包含了多个精确光源，我们可以把它们分别代入上面的式子进行计算，然后把它们的结果相加即可。也就是说，反射等式可以简化成下面的形式： \[ L_o(v)=\sum_{i=0}^{n}L_o^i(v)=\sum_{i=0}^{n}\pi f(l_c^i,v)c_{light}(n \cdot l_c^i) \] 那么，剩下的问题就是，\(f(l_c,v)\)项怎么算呢？\(f(l_c,v)\)实际上描述了当前点事如何与入射光线进行交互的：当给定某个入射方向的入射光后，有多少百分比的光照被反射到了观察方向上。在图形学中，这一项有一个专门的名字，那就是双向反射分布函数，即BRDF。

3、BRDF

BRDF可以用于描述两种不同的物理现象：表面反射和次表面散射。针对每种现象，BRDF通常会包含一个单独的部分来描述它们。用于描述次表面散射的被称为漫反射项，以及用于描述表面反射的部分被称为高光反射项。

（1）漫反射项

有很多种实现方式，这里直接给出下面会用到的公式： \[ f_{diff}(l,v)=\frac{baseColor}{\pi}(1+(F_{D90}-1)(1-n\cdot l)^5)(1+(F_{D90}-1)(1-n\cdot v)^5) \] 其中： \[ F_{D90}=0.5+2*roughness*(h\cdot l)^2 \] \(baseColor\)是表面颜色。通常由纹理采样得到，\(roughness\)是表面的粗糙度。

在Unity中的实现代码如下：

1
2
3
4
5
6
7
8
9
10
inline half3 CustomDisneyDiffuseTerm(half NdotV, half NdotL, half LdotH, half roughness, half3 baseColor)
{
    half fd90 = 0.5 + 2 * LdotH * LdotH * roughness;
    
    // Two schlick fresnel term
    half lightScatter = 1 + (fd90 - 1) * pow(1 - NdotL, 5);
    half viewScatter = 1 + (fd90 - 1) * pow(1 - NdotV, 5);
    
    return baseColor * INV_PI * lightScatter * viewScatter;
}

（2）高光反射项

基于微面元理论，BRDF的高光反射项科研用下面的通用形式来表示： \[ f_{spec}(l,v)=\frac{F(l,h)G(l,v,h)D(h)}{4*(n \cdot l)(n \cdot v)} \] 这就是著名的Torrane-Sparrow微面元模型。

\(D(h)\)是微面元的法线分布函数，它用于计算有多少比例的微面元的法线满足\(m=h\)，只有这部分微面元才会把光线从\(l\)方向反射到\(v\)方向上。

\(G(l,v,h)\)是阴影-遮掩函数，它用于计算那些满足\(m=h\)的微面元中有多少会由于遮挡而不会被人眼看到，因此它给出了活跃的微面元所占的浓度，只有活跃的微面元才会成功地把光线反射到观察方向上。

\(F(l,h)\)则是这些活跃微面元的菲涅尔反射函数，它可以告诉我们每个活跃的微面元会把多少入射光线反射到观察方向上，即表示了反射光线占入射光线的比率。

最后，分母\(4*(n \cdot l)(n \cdot v)\)是用于校正从微面元的局部空间到整体宏观表面数量差异的校正因子。

a、菲涅尔反射函数

大多数PBS实现选择使用Schlick菲涅尔近似等式来得到近似的菲涅尔反射效果： \[ F_{Schlick}(l,h)=c_{spec} + (1-c_{spec})(1-(l \cdot h))^5 \] 其中，\(c_{spec}\)是材质的高光反射颜色。在金属工作流和高光反射工作流中，\(c_{spec}\)的计算是不同的，这里要注意。

在Unity中的实现代码如下：

1
2
3
4
5
inline half3 CustomFresnelTerm(half3 c, half cosA)
{
    half t = pow(1 - cosA, 5);
    return c + (1 - c) * t;
}

b、法线分布函数

这里选择的法线分布函数是GGX分布，它的公式如下： \[ D_{GGX}(h)=\frac{\alpha ^ 2}{\pi ((\alpha ^2 -1)(n \cdot h)^2 + 1)^2} \] 其中： \[ \alpha = roughness^2 \] \(roughness\)是与表面粗糙度有关的参数。

在Unity中的实现代码如下：

1
2
3
4
5
6
inline half CustomGGXTerm(half NdotH, half roughness)
{
    half a2 = roughness * roughness;
    half d = (NdotH * a2 - NdotH) * NdotH + 1.0f;
    return INV_PI * a2 / (d * d + 1e-7f);
}

上面的\(1e-7f\)是为了避免分母为0。

c、阴影-遮挡函数

Unity为基于GGX的PBS模型改用了Smith-Joint阴影-遮挡函数，公式如下： \[ \frac{G_{smithJoint}(l,v,h)}{(n \cdot l)(n \cdot v)} \approx \frac{2} {(n \cdot l)((n \cdot v)(1-\alpha_g)+\alpha_g) + (n \cdot v)((n \cdot l)(1-\alpha_g)+\alpha_g)} \] 回顾上面高光反射项的公式： \[ f_{spec}(l,v)=\frac{F(l,h)G(l,v,h)D(h)}{4*(n \cdot l)(n \cdot v)} \] 可以发现，上面实现的并不单单是G项，还包括了分母的部分。所以上面的就不是纯粹的阴影-遮挡函数了，一般叫做可见性项。

在Unity中的实现代码如下：

1
2
3
4
5
6
7
8
inline half CustomSmithJointGGXVisibilityTerm(half NdotL, half NdotV, half roughness)
{
    half a2 = roughness * roughness;
    half lambdaV = NdotL * (NdotV * (1 - a2) + a2);
    half lambdaL = NdotV * (NdotL * (1 - a2) + a2);
    
    return 0.5f / (lambdaV + lambdaL + 1e-5f);
}

这里可以有些疑惑，代码的实现跟上面的公式不同啊？这是因为，把反射项的分母4也计算在内了。

二、IBL

为了得到更加真实的效果，还需要计算基于图形的光照部分（IBL）。

在Unity中一般是通过反射探针实现的。

1
2
3
4
5
6
7
//IBL
half perceptualRoughness = roughness * (1.7 - 0.7 * roughness);
half mip = perceptualRoughness * 6;
half4 envMap = SAMPLE_TEXTURECUBE_LOD(unity_SpecCube0, samplerunity_SpecCube0, reflDirWS, mip);
half grazingTerm = saturate((1 - roughness) + (1 - oneMinusReflectivity));
half surfaceReduction = 1.0 / (roughness * roughness + 1.0);
half3 indirectSpecular = surfaceReduction * envMap.rgb * CustomFresnelLerp(specColor, grazingTerm, nv);

主要就是根据粗糙度对环境贴图进行LOD采样。

为了给IBL添加更加真实的菲涅尔反射，我们对高光反射颜色和掠射颜色grazingTerm进行菲涅尔插值。除此之外，还使用了由粗糙度计算得到的surfaceReduction参数进一步对IBL进行修正。CustomFresnelLerp函数的代码如下：

1
2
3
4
5
inline half3 CustomFresnelLerp(half3 c0, half3 c1, half cosA)
{
    half t = pow(1 - cosA, 5);
    return lerp(c0, c1, t);
}

它的实现和回去实现的CustomFresnelTerm函数很类似，不同的是这里使用参数\(t\)来混合两个颜色。

最后，只需要按照渲染方程把所有项加起来即可。

1
2
half3 col = emissionTerm + PI * (diffuseTerm + specularTerm) * mainLight.color * nl * mainLight.distanceAttenuation * mainLight.shadowAttenuation
                + indirectSpecular;

三、两种工作流

在Unity实现的PBR中，包含了两种工作流：高光反射工作流、金属工作流。它们之间的区别，只是参数的获取方式不同，最后使用的渲染方程都是上面介绍的。下面分布介绍一下二者。

1、高光反射工作流

先看下属性：

1
2
3
4
5
6
7
8
9
_Color ("Color", Color) = (1, 1, 1, 1)
_MainTex ("Albedo", 2D) = "white" { }
_Glossiness ("Smoothness", Range(0.0, 1.0)) = 0.5
_SpecColor ("Specular", Color) = (0.2, 0.2, 0.2)
_SpecGlossMap ("Specular (RGB) Smoothness (A)", 2D) = "white" { }
_BumpScale ("Bump Scale", Float) = 1.0
_BumpMap ("Normal Map", 2D) = "bump" { }
_EmissionColor ("Color", Color) = (0, 0, 0)
_EmissionMap ("Emission", 2D) = "white" { }

比较特别的是，定义了高光反射的颜色和高光反射贴图。光滑值保存在_SpecGlossMap贴图的a通道中。高光颜色由_SpecColor和_SpecGlossMap的rgb通道相乘得到。

主要计算过程如下：

1
2
3
4
5
6
7
8
9
half4 specGloss = SAMPLE_TEXTURE2D(_SpecGlossMap, sampler_SpecGlossMap, input.uv);
specGloss.a *= _Glossiness;
half3 specColor = _SpecColor.rgb * specGloss.rgb;
half roughness = 1.0 - specGloss.a;

half oneMinusReflectivity = 1.0 - max(max(specColor.r, specColor.g), specColor.b);

half3 albedo = _Color.rgb * SAMPLE_TEXTURE2D(_MainTex, sampler_MainTex, input.uv).rgb;
half3 diffColor = albedo * oneMinusReflectivity;

然后就是根据公式进行计算。这里不再赘述。

代码如下

2、金属工作流

属性：

1
2
3
4
5
6
7
8
_Color ("Color", Color) = (1, 1, 1, 1)
_MainTex ("Albedo", 2D) = "white" { }
_Glossiness ("Smoothness", Range(0.0, 1.0)) = 0.5
_MetallicGlossMap ("Metallic", 2D) = "white" { }
_BumpScale ("Bump Scale", Float) = 1.0
_BumpMap ("Normal Map", 2D) = "bump" { }
_EmissionColor ("Color", Color) = (0, 0, 0)
_EmissionMap ("Emission", 2D) = "white" { }

与上面的高光反射工作流相比，大部分相同，只是使用_MetallicGlossMap代替了高光相关的两项。

_MetallicGlossMap的r通道保存的是金属值，a通道保存的是光滑值，而高光反射的颜色由kDieletricSpec和albedo通过金属值metallic插值得到。

1
2
3
4
5
6
7
8
9
10
half4 metallicMap = SAMPLE_TEXTURE2D(_MetallicGlossMap, sampler_MetallicGlossMap, input.uv);
half metallic = metallicMap.r;
half smoothness = metallicMap.a * _Glossiness;
half roughness = 1.0 - smoothness;

half3 albedo = _Color.rgb * SAMPLE_TEXTURE2D(_MainTex, sampler_MainTex, input.uv).rgb;

half oneMinusReflectivity = kDieletricSpec.a - metallic * kDieletricSpec.a;
half3 diffColor = albedo * oneMinusReflectivity;
half3 specColor = lerp(kDieletricSpec.rgb, albedo, metallic);

kDieletricSpec是URP中的内置变量，可以在Lightin.hlsl中找到：

1
#define kDieletricSpec half4(0.04, 0.04, 0.04, 1.0 - 0.04)

其他部分的计算与高光反射工作流都是相同的。

代码如下

四、总结

本文主要给出PBR的相关计算公式，然后给出计算代码。这里要注意，这些公式并不是唯一的。

还是说一下，本文相对来说还是很简单的介绍，建议阅读下面的参考部分。

参考

-------------本文结束感谢您的阅读-------------